4. 선박 산법(船舶算法)
선체가 복잡한 곡면으로 형성되어 있음을 앞에서 충분히 판단할 수 있었을 것이다. 복잡한 곡면으로 싸여 있는 선체는 구(球), 원통(圓筒), 각주(角柱) 등과 같은 단순한 기하학적 물체가 아니기 때문에 그 용적 또는 용적의 중심위치를 계산하기가 간단치 않다. 또한, 절단평면으로 얻은 수선면, 횡단면 같은 곡선도 간단한 대수학적인 수식으로 표현하기 불가능한 것들이다.
이런 곡선으로 싸여 있는 곡면의 면적, 용적 또는 그 중심위치를 계산하는데 있어서 조선공학에서는 2가지의 근사적분법(近似積分法)을 사용하고 있다. 하나는 계산에 의하여 구하는 방법이고, 다른 하나는 면적계(面積計; Planimeter)나 적기(積分器; Integlater)와 같은 기계를 이용하여 구하는 방법이다. 근래에는 선형을 수학적으로 표시해 보려고 노력하고 있으나 아직 실용단계에 이르지 못하고 있다.
선박의 용적도, 배수량, 총톤수, 복원성 등의 계산에 사용되는 기초적인 산법은 다음과 같다.
가. 면적계산
어떤 곡선으로 된 면의 정확한 면적을 순수한 수학적인 방법으로 계산하기 위하여는 곡선을 표시하는 방정식을 필요로 한다.
아래 그림의 곡선 EF가 다음과 같은 방정식으로 표시된다고 하자
y = f (x)
그러면 CDEF 의 면적 A는 다음과 같이 수식화 할 수 있다.
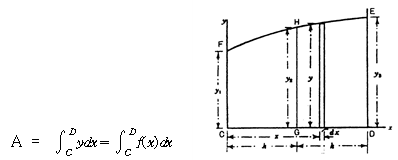
곡선 EF가 정확하게 방정식으로 표시될 경우에는 정확한 면적을 얻을수 있다. 그러나 선박에 사용되는 곡선은 방정식으로 표현되는 것이 거의 불가능하다. 따라서, 근사값을 쉽고 빨리 얻는 목적으로 다음과 같은 근사적분법이 이용된다.
1) 사다리꼴 법칙 (Trapezoidal rule)
아래 그림에서 곡선면 CDEF의 면적을 계산하기 위하여 등분간격 h로 밑변 CD를 4등분한 경우 CDEF의 근사 면적은 사다리꼴 C홀, GJKH, JLMK, LDEM의 면적을 합하여 얻을 수 있다.

따라서 CDFF의 총면적 A 는 다음과 같다.
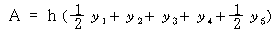
윗 식을 일반형으로 고쳐 쓰면 다음과 같다.

이를 사다리꼴법칙이라고 한다. 즉, 처음 종선과 마지막 종선의 길이의 반에 나머지 종선의 길이의 합계를 더하고 여기에 등분간격을 곱하면, 해당 곡서면의 면적을 얻을 수 있다.
2) 심슨 제1법칙 (Simpson´s First Rule)
아래 그림에서 곡선 FHE를 2차 포물선이라 가정하면 곡선 FHE의 방정식은 다음과 같이 표시될 수 있다.
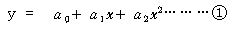
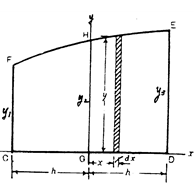
기선 CD를 x축, CD의 2등분선 GH를 y축으로 잡으면 곡선면 CDEF의 면적 A는 다음과같다.


이 식을 Simpson의 제1법칙이라 부르며, 이것을 말로 표현하면 다음과 같다.
즉, 양끝에 있는 종선의 길이의 합계에 홀수번째의 종선의 길이의 2배를 합하여 더하고, 짝수번째의 종선의 길이의 4배를 합하여 더한 것에 등분간격의 1/3을 곱한 것이다. 이 때 주의할 것은 도형의 등분수는 반드시 짝수로해서 종선의 수를 홀수 개(2n+1)로 만들어야 하며, 종선사이의 등분간격을 작게하여 이 사이의 곡선의 변화가 2차이하의 방정식으로 표현될 수 있도록 하여야 한다. 만일 국부적으로 곡선의 변화가 심할 경우에 는 그 부분을 세분하고 보조분할 종선을 세워 계산의 정확성을 가하여야 한다. 일반적으로 선체의 선수, 선미부분은 수선의 기울기가 심하므로 이 부근의 구분은 더 세분하여 보조분할종선을 증설하는 것이 좋다. 보조분할종선을 증설하였을 때에는 종선의 길이에 곱하여야 할 계수가 변하므로 주의를 요한다.

'선박개론' 카테고리의 다른 글
| 5. 선박의 톤수 (0) | 2023.03.12 |
|---|---|
| 배수량, 부심(부심의 위치), 매센티당배수톤(TPC) (0) | 2023.03.12 |
| 선박의 형상계수(방형계수, 주형계수, 중앙횡단면계수, 수선면계수, 수직주형계수) (0) | 2023.03.09 |
| 선박의 흘수와 트림 (0) | 2023.03.08 |
| 선박의 주요 치수 (0) | 2023.03.08 |




댓글